

توضیحات
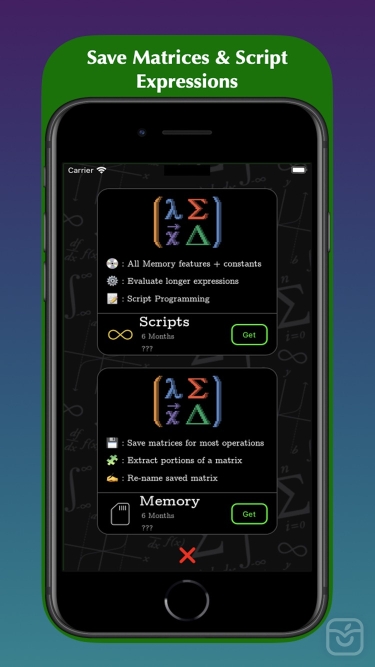
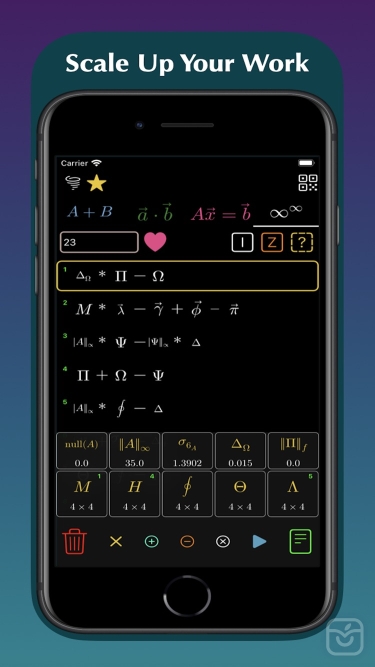
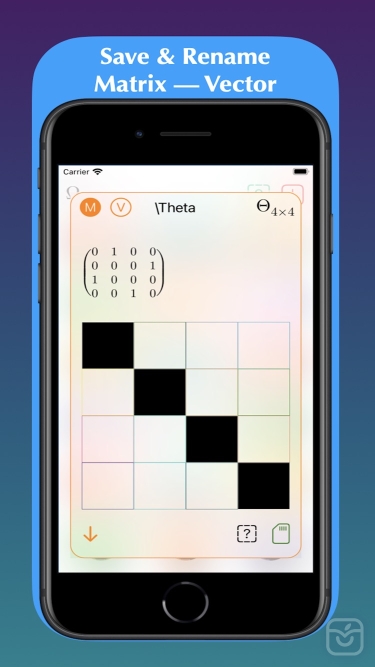
Matrix Numerics is a powerful Numerical Linear Algebra app with a simple and user-friendly interface. It is designed to quickly present you Linear Algebra results involving matrices and vectors with the fewest taps possible. Matrix Numerics uses the SwiftLAN engine to approximate solutions to a linear system of equations, compute matrix decompositions and calculate vector dynamics. SwiftLAN is a powerful Linear Algebra framework developed by academics for the purpose of native Scientific Computation and Modeling in Swift. Its State-of-the-art Numerical algorithms take advantage of the expressiveness and lightning speed of the Swift programming language to deliver powerful performance and accuracy. Each algorithm in the framework is extensively researched, developed and debugged following closely the mathematical literature of authors like G. Golub, D.S Watkins, J.G.F Francis, C. Van Loan and many others. After development, all algorithms are written 100% in Swift and are intensively tested for speed and accuracy against MATLAB, Accelerate and the LAPACK++ library in C++. All of these aspects make Matrix Numerics a world class tool for scientists, students or any other person exposed to Linear Algebra no matter how early are they in their scientific/mathematical carries. These are some of the things you can do on Matrix Numerics:
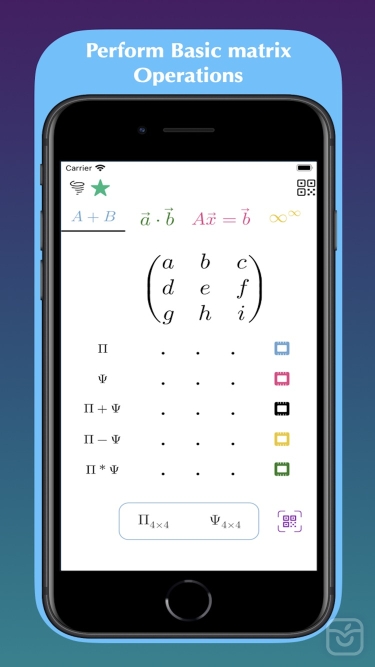
- Add, subtract, multiply matrices.
- Inverse
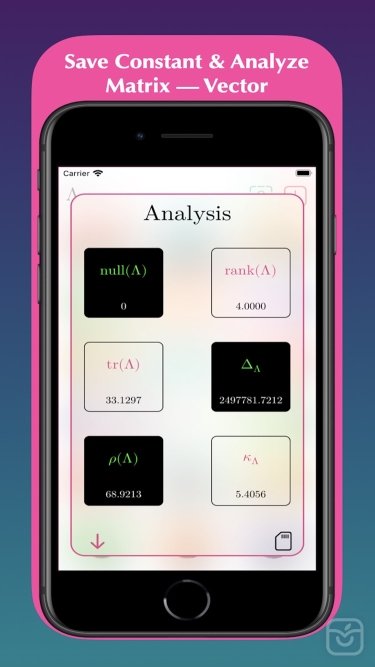
- Condition Number
- Rank
- Spectral Radius
- Trace
- Determinant
- Transpose
- Adjoint
- Characteristic Polynomial
- Eigenvalues & Eigenvectors
- Singular Values
- Singular Value Decomposition
- Pseudoinverse
- PLU Decomposition
- Cholesky Decomposition
- Gram-Schmidt Decomposition
- QR Decomposition
- Upper Hessenberg Decomposition
- Real Schur Form Decomposition
- Norms 1,2,Infinity and Frobenius.
- Fundamental Subspaces
When dealing with Vectors, Matrix Numerics can help you compute:
- Inner Product
- Cross Product
- Projection Vector
- Correlation between vectors
- Angle between vectors
- Vector Length
- Vector Normalization
- Vector Orthonormalization
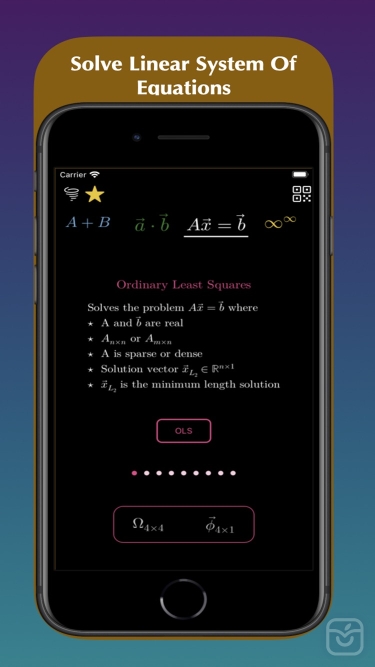
You can also approximate solutions to Linear System of Equations and Linear Least Squares using the algorithm that best fits your system:
- Ordinary Least Squares
- Iteratively Reweighted Least Squares
- Pseudoinverse by SVD
- Kaczmarz’s Algorithm
- PLU with Scaled Row Pivoting
- Successive Over Relaxation
- Conjugate Gradient
- Gauss-Seidel Iteration
- Jacobi Iteration
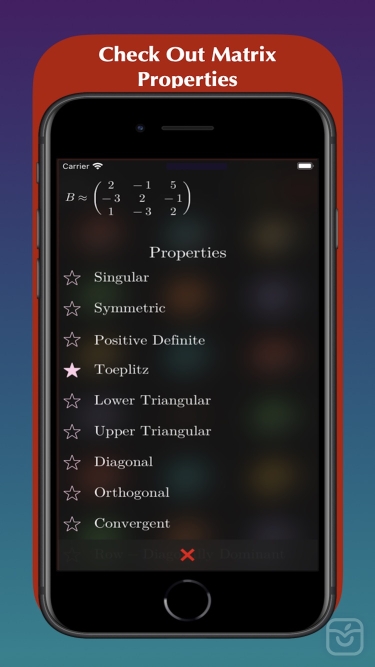
Identify specific attributes of your System/Matrix with a single touch:
- Is it Singular?
- Is it Symmetric?
- Is it Positive Definitive?
- Is it Diagonal?
- Is it Upper or Lower Diagonal or both?
- Is it Orthogonal?
- Is it Convergent?
- Is it Row or Column Diagonally Dominant or both?
Numerical results and notations are beautifully rendered in a LaTeX-like style supporting both decimal and rational modes. All matrix computations are preformed in-device on the powerful A-Series Apple chips which means you can use Matrix Numerics everywhere and anywhere with no internet connection required!! Matrix Numerics works on iPhone 6 or newer and all iPads except mini.
Special thanks to J. Dominguez, L. Meza & L. Smith.
For more information about Privacy, Subscriptions and Terms of use please refer to the following:
Privacy: https://docs.google.com/document/d/1WSpjT6VbJVA55r36gqsAb3KwGTRvVjfvx2zQKSdliYk/edit?usp=sharing
Terms of Use: https://docs.google.com/document/d/146K3w6323RK6ipXVsjiWpP1owpQC8SJNSjgeAdShtsc/edit?usp=sharing
تغییرات نسخه اخیر
Added support for iOS 15
Added support for iPad Mini 6th Gen.
توسعه دهنده
Horacio Sanchez

